A spherical snowball is melting in such a way – Embarking on an exploration of a spherical snowball’s melting process, this discourse unveils the captivating interplay of physical properties, heat transfer, and fluid dynamics. Delving into the intricate mechanisms at play, we unravel the secrets behind this seemingly mundane phenomenon, revealing its profound implications for diverse fields.
As the spherical snowball surrenders to the relentless embrace of warmth, its physical characteristics undergo a metamorphosis. The once-pristine orb gradually relinquishes its spherical form, its surface area expanding as its volume diminishes. This transformation is governed by the interplay of temperature, humidity, and wind speed, each exerting a subtle influence on the rate of melting.
Physical Properties of a Melting Spherical Snowball
A spherical snowball is a compact, spherical mass of snow that is formed by the accumulation and compression of snow crystals. The shape and size of a spherical snowball can vary depending on the amount of snow available, the temperature, and the amount of compaction.
As a spherical snowball melts, its volume decreases while its surface area increases. The rate of melting is influenced by several factors, including the temperature, humidity, and wind speed.
Factors Affecting the Rate of Melting
- Temperature:The higher the temperature, the faster the snowball will melt.
- Humidity:The higher the humidity, the slower the snowball will melt.
- Wind speed:The higher the wind speed, the faster the snowball will melt.
Heat Transfer and Thermodynamics
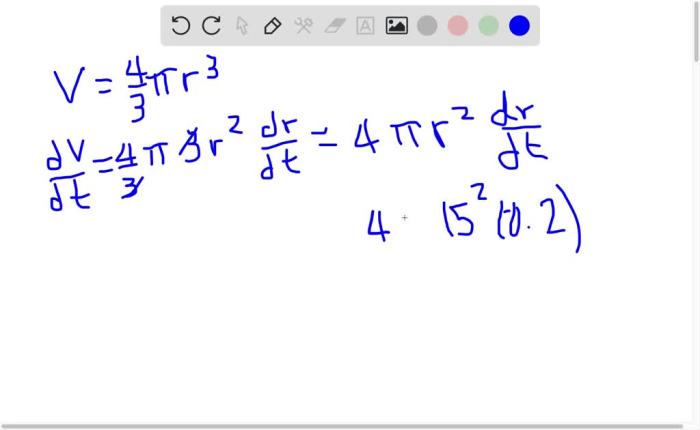
The melting of a spherical snowball involves several modes of heat transfer, including conduction, convection, and radiation. Specific heat capacity is the amount of heat required to raise the temperature of a unit mass of a substance by one degree Celsius.
Latent heat is the amount of heat required to change the phase of a substance without changing its temperature. The energy balance equation for the melting snowball can be used to calculate the rate of melting.
Energy Balance Equation
$$\fracdQdt = hA(T_a
- T_s) + \epsilon \sigma A(T_a^4
- T_s^4) + L\fracdmdt$$
- $$\fracdQdt$$ is the rate of heat transfer
- $h$ is the convective heat transfer coefficient
- $A$ is the surface area of the snowball
- $T_a$ is the ambient temperature
- $T_s$ is the surface temperature of the snowball
- $\epsilon$ is the emissivity of the snowball
- $\sigma$ is the Stefan-Boltzmann constant
- $L$ is the latent heat of fusion of ice
- $\fracdmdt$ is the rate of mass loss due to melting
Surface Tension and Capillary Action

Surface tension is the force that causes the surface of a liquid to behave like a stretched elastic membrane. The surface tension of water acts to minimize the surface area of the melting snowball. Surface tension also affects the shape and behavior of the melting water droplets.
Capillary action is the movement of water through a porous material due to the surface tension of the water. Capillary action can play a role in the movement of water through the snowball.
Surface Tension Forces, A spherical snowball is melting in such a way
- Cohesive forces:Forces that act between molecules of the same substance, holding them together.
- Adhesive forces:Forces that act between molecules of different substances, attracting them to each other.
Hydrodynamics and Fluid Flow

The melting water flowing over the surface of a spherical snowball can be described by the principles of fluid dynamics. The fluid dynamics of the melting water can be used to predict the formation and behavior of rivulets and droplets on the snowball’s surface.
The flow patterns and velocity profiles of the melting water can also be analyzed.
Flow Patterns
- Laminar flow:Smooth, orderly flow in which the fluid moves in layers, with no disruption between the layers.
- Turbulent flow:Chaotic, irregular flow in which the fluid moves in eddies and swirls.
Numerical Modeling and Simulation
Numerical modeling and simulation can be used to study the melting process of a spherical snowball. Numerical simulations can be used to predict the rate of melting, the shape of the melting snowball, and the flow patterns of the melting water.
However, numerical simulations can be computationally expensive and time-consuming.
Challenges and Limitations
- Computational cost:Numerical simulations can be computationally expensive, especially for complex models.
- Model accuracy:The accuracy of numerical simulations depends on the accuracy of the model and the input data.
- Model validation:Numerical simulations should be validated against experimental data to ensure their accuracy.
Applications and Implications

Understanding the melting process of a spherical snowball has applications in fields such as snow hydrology, cryospheric science, and engineering. The melting process of snowballs can be used to predict the rate of snowmelt, the formation of avalanches, and the stability of snowpack.
The melting process of snowballs can also be used to design snow-melting systems and to develop new methods for snow removal.
Implications for Snowpack Stability
- Rapid melting:Rapid melting of snowballs can lead to the formation of meltwater, which can lubricate the snowpack and increase the risk of avalanches.
- Snowpack stability:The stability of snowpack is influenced by the rate of melting of snowballs.
FAQ Overview: A Spherical Snowball Is Melting In Such A Way
What factors influence the rate of melting of a spherical snowball?
The rate of melting is primarily influenced by temperature, humidity, and wind speed. Higher temperatures accelerate the melting process, while higher humidity and wind speed can slow it down.
How does surface tension affect the melting process?
Surface tension forces act on the surface of the melting snowball, causing water droplets to form and behave in a unique manner. These forces influence the shape and movement of the water droplets.
What are the applications of understanding the melting process of a spherical snowball?
Understanding the melting process has applications in fields such as snow hydrology, cryospheric science, and engineering. It helps in predicting snowpack stability, managing water resources, and developing snow removal techniques.